Backtracking

Exhaustive Search(穷举搜索)

现在很多方法可以进行穷举搜索，比如枚举、递归、回溯等。

但是对于某些问题,您可以用递归来进行穷举搜索，但是递归的层数太多，会导致栈溢出。

---

小练习:输出你想要位数的二进制数

这时候我们就会用到“树”的概念。

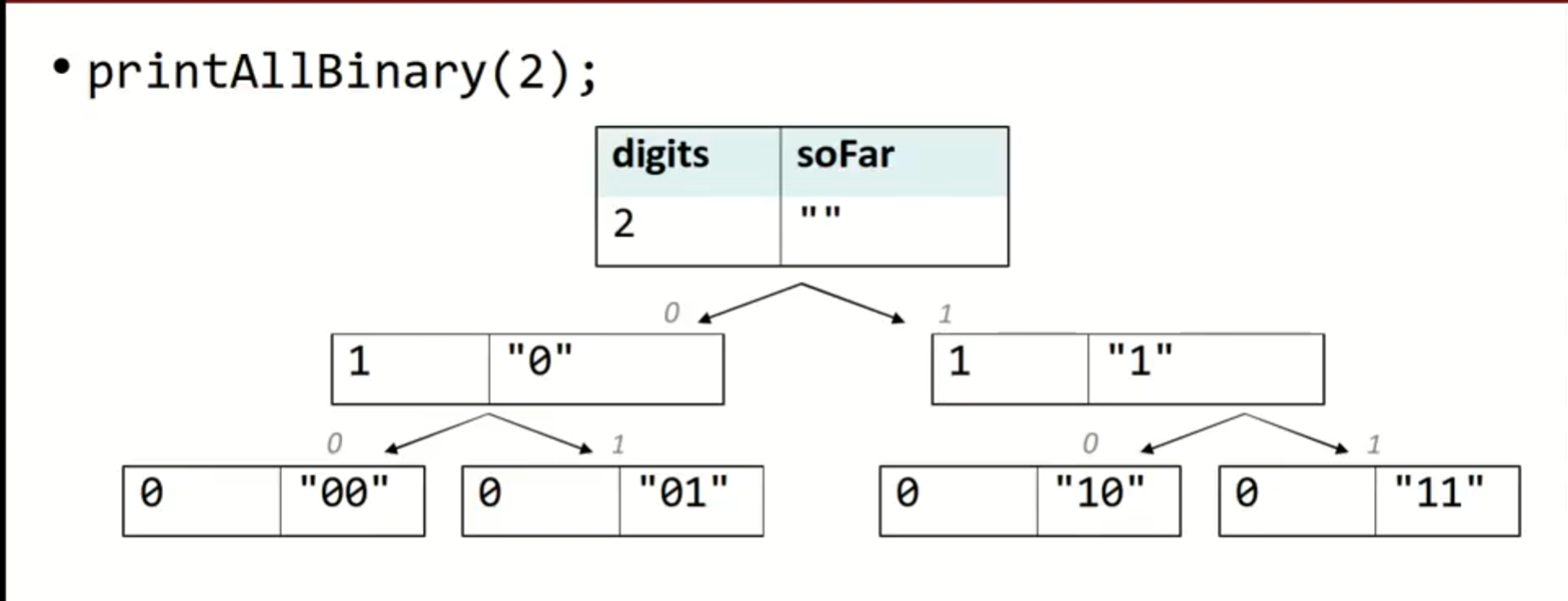
我们可以用递归来实现这个过程。

void printBinaryHelper(int digits, string output) {
    if (digits == 0) {
        cout << output << endl;
    } else {
        printBinaryHelper(digits - 1, output + "0");
        printBinaryHelper(digits - 1, output + "1");
    }

}

void printBinary(int digits) {
    printBinaryHelper(digits, "");
}

这个函数的作用是输出从 0 到digits位的二进制数。

我们可以调用printBinary(3)来输出 0 到 3 位的二进制数。

000
001
010
011
100
101
110
111

Backtracking(回溯)

回溯是一种算法，它是一种穷举搜索的变体,称为回溯法

通过尝试部分解决方案来寻找解，并在不合适时放弃它们。

• 一种“暴力”算法技术（尝试所有路径）
• 通常采用递归实现

尝试多种可能性，如果进展不如意就回溯

和穷举类似,只是在其中还需要执行一个所谓的"撤销选择"的操作.

小练习:投色子游戏

例如:diceSum(2,7)

{1,6}
{2,5}
{3,4}
{4,3}
{5,2}
{6,1}

我们可以用回溯法来实现这个过程。

void diceSumHelper(int dice, int desiredSun, Vector<int>& chosen)
{
    if (dice == 0) {
        if (destiredSun == 0) {
            cout << chosen << endl;
        }
    }
    else {
        for (int i = 1; i <= 6; i++) {
            chosen.add(i);
            diceSumHelper(dice - 1, desiredSun - i,chosen);
            chosenremoveBack();
        }
    }
}

这个函数的作用是输出从 1 到 6 的骰子的组合，使得骰子的和等于desiredSun。

我们可以调用diceSumHelper(2,7)来输出 2 个骰子的组合。

{1,6}
{2,5}
{3,4}
{4,3}
{5,2}
{6,1}

可是这个算法有什么问题呢?

• 它会产生大量的重复计算，导致效率低下
• 它会产生大量的回溯，导致效率低下
• 它会产生大量的内存消耗，导致效率低下

总而言之效率低下

这就是所谓的暴力求解!