Binary Search Trees(二叉搜索树)

Traversals(遍历)

遍历可谓是任何数问题的最佳途径

对于任何的树型问题,你都需要进行一种操作,即审视节点及其子节点.

常见的遍历有三种:

1. 前序遍历(Preorder Traversal): 先访问根节点,再访问左子树,最后访问右子树.
2. 中序遍历(Inorder Traversal): 先访问左子树,再访问根节点,最后访问右子树.
3. 后序遍历(Postorder Traversal): 先访问左子树,再访问右子树,最后访问根节点.

实例:

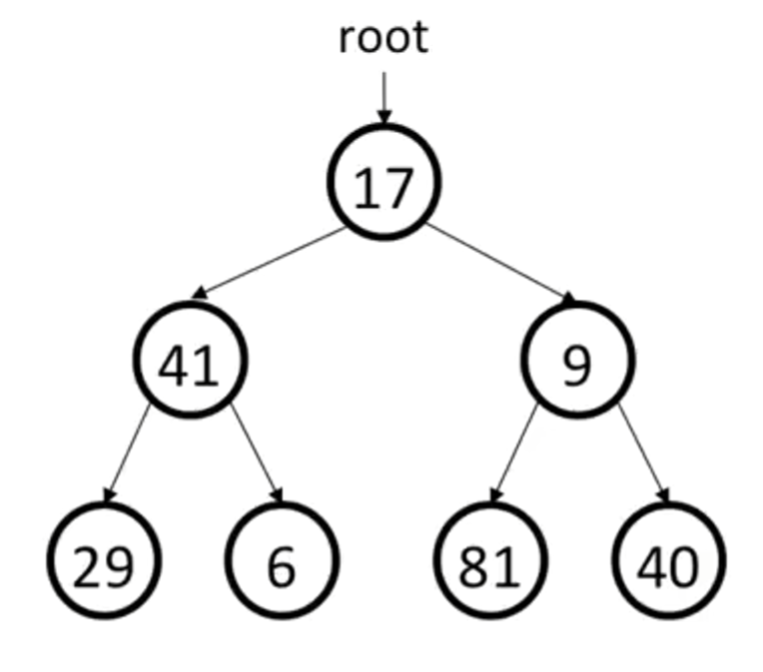
• 前序排列:17 41 29 6 9 81 40

• 中序排列:29 41 6 17 81 9 40

• 后续排列:29 6 41 81 40 9 17

void preorder(Node* root) {
    if (root == NULL) return;
    cout << root->data << " ";
    preorder(root->left);
    preorder(root->right);
}//前序遍历

void inorder(Node* root) {
    if (root == NULL) return;
    inorder(root->left);
    cout << root->data << " ";
    inorder(root->right);
}//中序遍历

void postorder(Node* root) {
    if (root == NULL) return;
    postorder(root->left);
    postorder(root->right);
    cout << root->data << " ";
}//后序遍历

Contains(查找)

查找操作是二叉搜索树的基本操作之一.

解决方法依旧是使用遍历

bool contains(TreeNode* node, int value){
    if(node == nullptr) return false;
    else if (node->date == value) return true;
    else{
        return contains(node->left, value);
        return contains(node->right, value);
    }
}

这是如果运行你姐会发现问题

在递归调用的 else 分支中，您分别调用了 contains(node->left, value) 和 contains(node->right, value)，但它们是分开写的 return 语句。由于函数遇到第一个 return 语句后会直接返回，导致对右子树的检查永远不会执行。

bool contains(TreeNode* node, int value) {
    if (node == nullptr) return false;
    if (node->date == value) return true;
    // 如果左子树中找到，返回 true；否则检查右子树
    return contains(node->left, value) || contains(node->right, value);
}

如果这样写就不会有问题

Binary Search Tree (二叉搜索树)

简称 BST,是一种二叉树，其中每个非空节点 R 具有以下属性：

• R 的左子树中的每个元素包含的数据小于 R 的数据，

• R 的右子树中的每个元素包含的数据大于 R 的数据。

• R 的左子树和右子树也是二叉搜索树。

使用二叉搜索树可以实现快速查找、插入和删除操作，时间复杂度为 O(log n)。

为什么呢?

如果使用二叉搜索树,我们就可以用类似于二分法的方式来查找元素。

只需要查找树的一次,这样的查找自然比遍历整个树要快得多。

bool contains(TreeNode* node, int value) {
    if (node != nullptr) {
        if (node->data == value) {
            return true;
        } else if (node->data > value) {
            return contains(node->left, value);
        } else {
            return contains(node->right, value);
        }
    }
    return false;
}

二叉搜索树获取最大最小值非常的容易,只需要分别从根节点的左右子树中进行查找即可。

Adding To BST(添加)

和查找类似,我们只需要找到合适的位置,然后插入即可。

void add(TreeNode*& node, int value) {
    if (node == nullptr) {
        node = new TreeNode(value);
    } else if (node->data > value) {
        add(node->left, value);
    } else if (node->data < value) {
        add(node->right, value);
    }
}

Deleting From BST(删除)

删除操作也很简单,只需要找到要删除的节点,然后将其替换为它的后继节点,或者它的前驱节点。

如果要删除的节点没有子节点,那么直接将其删除即可。

如果要删除的节点只有一个子节点,那么直接将其子节点替换为其位置即可。

如果要删除的节点有两个子节点,那么找到后继节点,然后将其替换为要删除的节点,然后删除后继节点。

void deleteNode(TreeNode*& node, int value) {
    if (node == nullptr) return;
    if (node->data == value) {
        if (node->left == nullptr && node->right == nullptr) {
            delete node;
            node = nullptr;
        } else if (node->left == nullptr) {
            TreeNode* temp = node;
            node = node->right;
            delete temp;
        } else if (node->right == nullptr) {
            TreeNode* temp = node;
            node = node->left;
            delete temp;
        } else {
            TreeNode* temp = getSuccessor(node->right);
            node->data = temp->data;
            delete temp;
        }
    } else if (node->data > value) {
        deleteNode(node->left, value);
    } else {
        deleteNode(node->right, value);
    }
}

TreeNode* getSuccessor(TreeNode* node) {
    while (node->left != nullptr) {
        node = node->left;
    }
    return node;
}

Free Tree(释放树)

为了避免在丢弃树时泄漏内存，我们必须释放每个节点的内存。

像大多数树问题一样，通常是递归地编写。

必须释放节点本身及其左/右子树。

这也是树的另一种遍历。

void freeTree(TreeNode* node) {
    if (node == nullptr) return;
    freeTree(node->left);
    freeTree(node->right);
    delete node;
}