Backtracking 第三讲

选择,探索,撤销选择

回顾之前的笔记,我想最重要不过是这句话:选择,探索,撤销选择

关于递归风格

一个术语叫做:arm's length recursion(一臂之遥递归)

在人们编写递归代码的时候,他们往往回味代码添加不必要的复杂性

通常意味着那些无需存在的 if-else 语句,或者无用的变量,或者无用的函数调用

通常由另一种方式来组织这类代码结构，这也就是这门课程开设的意义

练习

所有子集

给定一个集合 S,求出 S 的所有子集。

例如: S =

所有子集:

{1,2,3}
{1,2}
{1,3}
{1}
{2,3}
{2}
{3}
{}

这和上一节的题目比较类似,但是也有很大的不同

解法

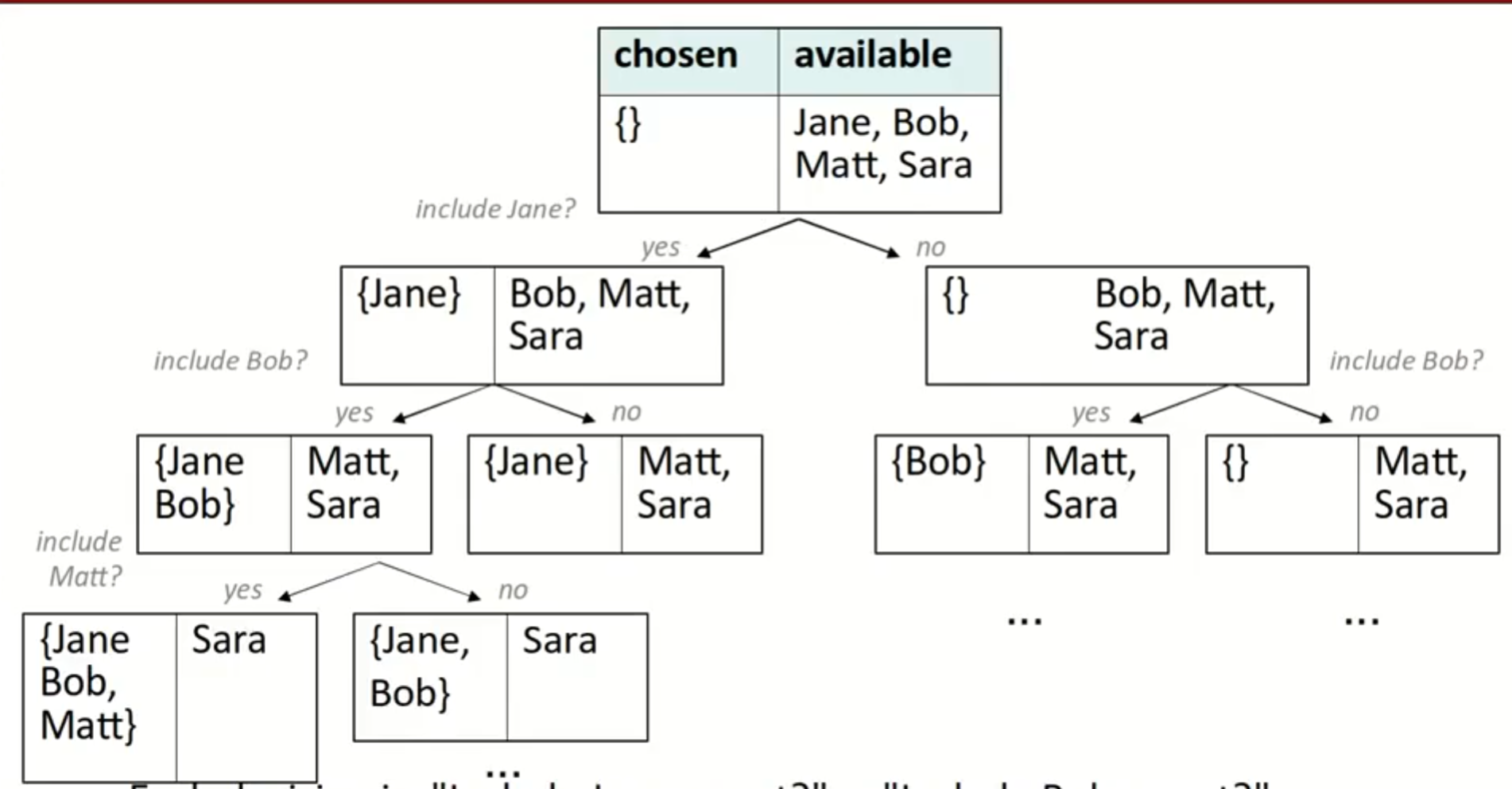
和调用树,决策树不同,两条分支,并非四条.

我们应该这样来写

void sublistHelper(Vector<string>& v, Vector<string>& chosen)
{
    if (v.isEmpty())
    {
        cout << chosen << endl;
    } else {
        string s = v[0];
        v.remove(0);

        //- 选择and探索(一个有s, 另一个没有s)
        sublistHelper(v, chosen);

        chosen.add(s);

        sublistHelper(v, chosen);


        //- 撤销选择
        v.insert(0, s);
        chosen.remove(chosen.size() - 1);//删除最后一个元素
    }
}

---

8 皇后问题

八皇后问题是一个经典的回溯问题,它要求在一个 8x8 的棋盘上摆放八个皇后,使得任何两个皇后都不能互相攻击.

解法

1. 首先,我们可以用一个二维数组来表示棋盘,其中每个元素的值表示皇后所在的列数.

2. 然后,我们可以用一个数组来表示皇后所在的行数,因为每行只能放一个皇后.

3. 我们可以用一个函数来表示是否可以放置皇后,这个函数的输入是列数,输出是是否可以放置.

4. 我们可以用一个函数来表示是否有冲突,这个函数的输入是两个皇后所在的行数,列数,输出是是否有冲突.

5. 我们可以用一个函数来表示摆放下一个皇后,这个函数的输入是棋盘,皇后所在的行数,输出是是否成功摆放.

6. 我们可以用一个循环来表示所有可能的摆放,每次都调用上面的函数来尝试摆放下一个皇后,如果成功,则继续摆放下一个皇后,如果失败,则回溯到上一个皇后.

7. 最后,我们可以用一个循环来表示所有可能的皇后位置,每次都调用上面的函数来尝试摆放八个皇后,如果成功,则输出结果,如果失败,则继续尝试下一个皇后位置.

#include <iostream>
#include <vector>

using namespace std;

const int N = 8;

bool isValid(int row, int col)
{
    for (int i = 0; i < col; i++)
    {
        if (row == i || abs(row - i) == abs(col - i))
        {
            return false;
        }
    }
    return true;
}

bool placeQueen(vector<int>& queens, int row)
{
    for (int col = 0; col < N; col++)
    {
        if (isValid(row, col))
        {
            queens[row] = col;
            if (row == N - 1)
            {
                return true;
            }
            if (placeQueen(queens, row + 1))
            {
                return true;
            }
        }
    }
    return false;
}

void printQueens(vector<int>& queens)
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            if (queens[i] == j)
            {
                cout << "Q ";
            } else {
                cout << "* ";
            }
        cout << endl;
    }
}

int main()
{
    vector<int> queens(N, -1);
    for (int i = 0; i < N; i++)
    {
        if (placeQueen(queens, i))
        {
            printQueens(queens);
            return 0;
        }
    }
    cout << "No solution found." << endl;
    return 0;
}

总结

回溯算法是一种非常强大的算法,它可以用来解决很多问题,但是它的实现方式却很有特点,需要我们对递归的理解更加深刻.