MSTs

最小生成树

最小生成树（Minimum Spanning Tree, MST）是一种用来连接所有顶点的无环连通图的树，它具有以下两个性质：

1. 连接所有顶点的最小权重的边。
2. 树中任意两个顶点间的路径上边的权重之和最小。

Kruskal 算法

Kruskal 算法是一种贪心算法，它通过按权重从小到大选择边，并保证所选边不形成回路，来构造最小生成树。具体步骤如下：

1. 按权重从小到大排序所有边。
2. 选择权重最小的边
3. 如果该边不形成回路，则将其加入最小生成树中，否则舍弃该边。

Graph Implementation

Edge list

图中所有边的无序列表。

它可以是一个数组，向量，链表或者结合

每条边存储起始/结束顶点。

顶点并没有被明确地存储在任何地方；顶点集 V 隐式包含在边缘列表中。

使用边缘列表你可以做到

• 给定顶点的所有邻居？一个给定顶点的度数？
• 是否存在从 A 到 B 的边？
• 是否存在自环（自边）？

Adjacency list

图中每个顶点的邻居列表。

就像这样：

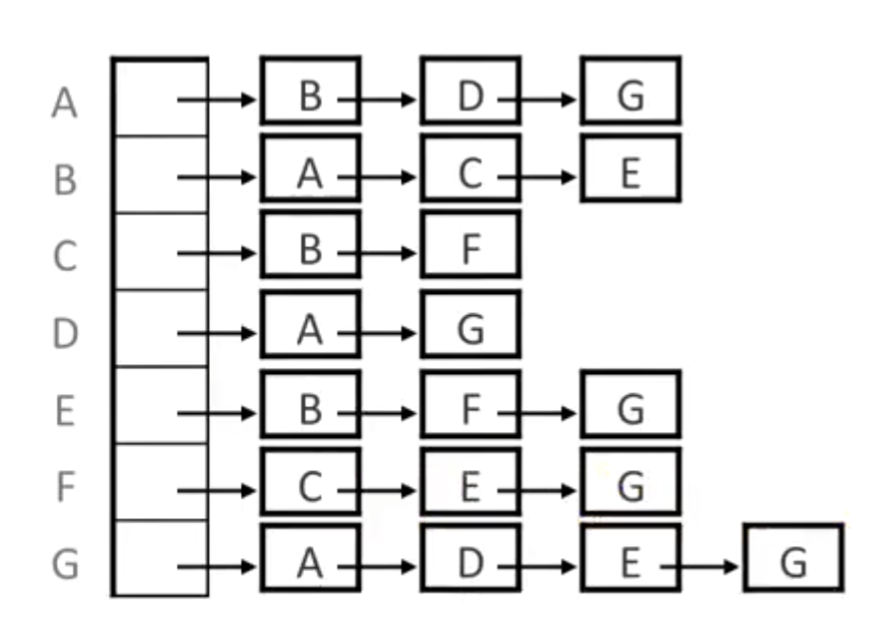
每条边存储起始/结束顶点，以及权重。

和上面的 Edge list 相比

Adjacency matrix

图中每个顶点的邻居矩阵。

k[i][j] 表示顶点 i 到顶点 j 的权重。

0 表示不存在边。

1 表示存在边。

如果是无向图，则 k[i][j] = k[j][i]。

如果边存在权重，这数组内部存储权重，不连接就取无限(也有的取无限大)